Physics - Intro to Projectile Motion Continues

LEARNING OBJECTIVES:

• I will practice doing trig problems today
• I will apply trig to projectile motion

CALENDAR:

 

WORDS O' THE DAY:

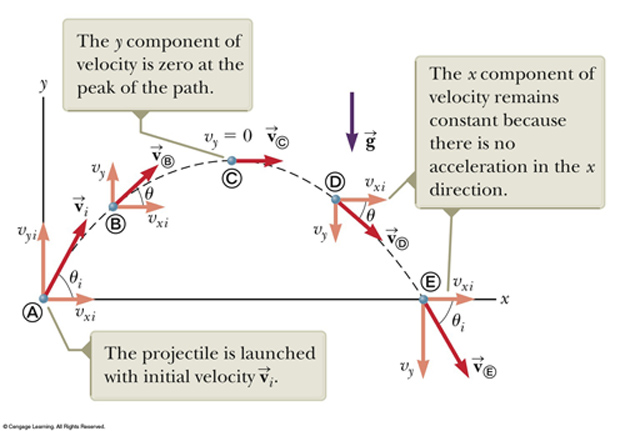
• Projectile Motion - Up/Vertical (y motion) AND Out/Horizontal (x motion)

FORMULAE OBJECTUS:

0) x_f = vt

1) v_f = v_i +at

2) v_avg = (v_i + v_f)/2

3a) x_f = x_i + v_it + 1/2at²

3b) y_f = y_i + v_it + 1/2at²

4) v_f² - v_i² = 2a∆x

4b) v_f² - v_i² = 2a∆y

WORK O' THE DAY:

Recall the following worksheet.

A coupla days ago we worked to find the length of the sides opposite a given angle (using Sin) and the length of the sides adjacent to a given angle (using Cos) for the following problems:

1, 2, 5, 7, 8 & 10.

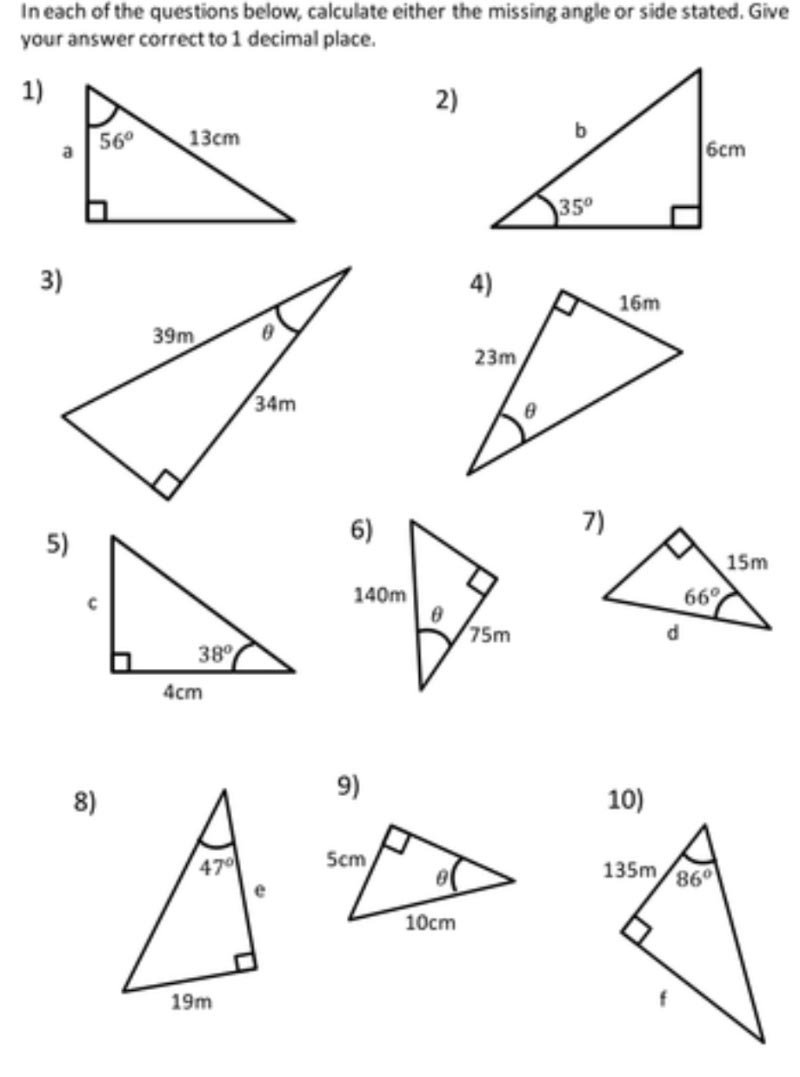
But what about the other problems?

Those problems ask us to find the ANGLE if we know the sides. In other words, we'll be doing the opposite operation.

In math, we call 'opposite' operations "INVERSE" operations. You may have noticed the INV Sin, Inv Cos and Inv Tan keys on your calculator. We use those to find the angles in a triangle if we know at least two sides of a triangle such as problem #9 above

══════════════════════════════

Let's take a look at that problem now:

Note the location of theta-- we know the length of the triangle opposite that angle is 5 cm. We also know the hypotenuse of the triangle is 10 cm.

So let's write out the definition of Sin:

Sinex = opp/hyp

Sinex = 5 cm/10 cm

Sinex = .5

We are trying to find theta so at this point we use the INVERSE operation to do that by using the 2nd key on our calculator so activate the INV Sin function.

.5 [INV][SIN] = 30

Which is the INVERSE of Sin 30 = .5 !!!

Please do the remaining problems on the worksheet now using the INVERSE functions to find the missing angles.

═══════════════════════════

Let's apply that new found knowledge go a more physics-ish problem:

You launch a frozen grape with an initial velocity of 26.6 m/s. The horizontal componant of that motion was 14.4 m/s. What angle did you launch at?

 

You launch a frozen grape with an initial velocity of 38.8 m/s. The horizontal componant of that motion was 24.4 m/s. What angle did you launch at?

 

Now let's try another projectile motion problem:

 

You launch a grape with an initial velocity of 41.1 m/s at an angle of 27 degrees. Let's further say that you launch the grape from the ground and the grape goes up and out and lands on the ground some distance away:

How high does the grape go?

How long does it take to get there?

How far away does the grape land?

═══════════════════════════

NOW let's mix it up a wee bit (well more than a wee bit!):

You are on top of a 34 meter tall building. You launch a grape at an angle of 29 degrees with an initial velocity of 45.55 m/s.

Please work with your group to DISCUSS a plan of attack BEFORE you get started. This will get a wee bit nasty! GOOD LUCK!

How high does the grape go?

How long does it take to get there?

How far away does the grape land?